• 概要・news
• シフトしたプレーン
• 再帰的な分割
• まとめ

再帰的な分割

次に Geohash の再帰的な矩形領域の分割に対してこの方法が問題を生じない事を示す。 説明と図を簡単にするために横方向についてだけ再帰的に 1/2 サイズに分割していけることを記すが、縦方向と合わせて矩形を四分割し続けることに問題がないことは自明であろう。（そこに穴があったり？）

クリックするとフルサイズの画像が得られます。

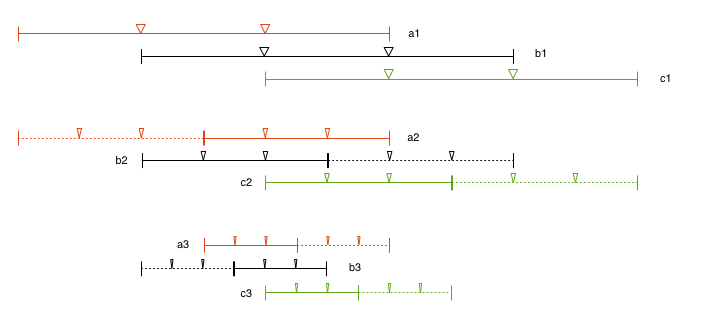	まずある粒度で分割された線分 a1 があったとする。これに対して 1/3 ずつズレた位置にある線分を b1, c1 とする。a1 の左には同じ長さの a1(-1), a1(-2) が連続的に存在するものとする。右にも同様に a1(1), a1(2) が存在するものとする。b, c プレーンについても同じ。 a2 （実線部分）は a1 を 1/2 に分割したもの（の右辺）である。b2, c2 も同様に一階上の線分を 1/2 にしたものである。a3, b3, c3 はそれぞれ a2, b2, c2 をやはり一階、階層的に分割した線分である。
まず a1, b1, c1 の階層を見ると、水平線上のどの地点であったとしても、必ず端に近くない領域（更に言えば左右 1/3 ずつの領域でなく、中央 1/3 の領域）に含まれる線分をみつけられる。 またそれが a2, b2, c2 の階層でも、a3, b3, c3 の階層でも同じくそのような線分を見つけられることがわかる。 つまりどのような階層であっても、再帰的に分割して行く限り任意の地点は必ずどこかのプレーンの中央 1/3 の領域に含まれることになる。
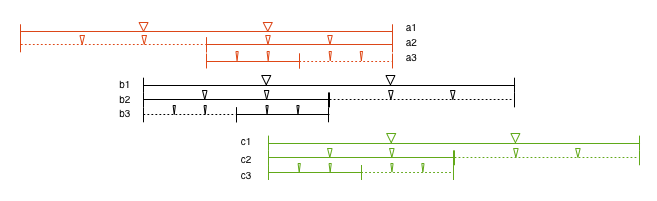	左に分かりやすさのために上の線分を並べ替えたものを示す。 線分は1/2 ずつ再帰的に分割されており、任意の地点について、すべての分割粒度（階層）で中央 1/3 に属する線分をみつけられるはずである。 （図をわかりやすくするために省いているが、全ての線分において描画されていない左右隣には同じ長さの線分が連続していることに注意）

最大粒度の矩形領域

なお、Geohash の最大矩形領域の取り方が変わると想像されるので注意されたい。
（筆者は Geohash のアイディアだけを聞いて思いついて書いているだけで、実際の Geohash データがどのような形態で取られているのかは知らない。全く的を外していたらごめんなさい。）

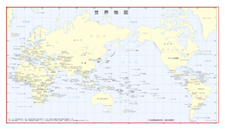	従来的には最大矩形領域（赤枠）がメルカトル図法での地図の最大領域をカバーするようにとるものと想像する。（繰り返し：外していたらごめんなさい。知らないのです。）
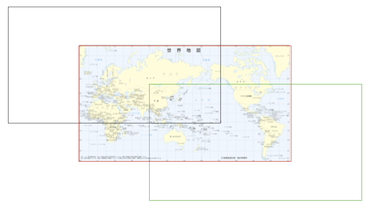	そのまま先に示してきたプレーンの割り当て方法を想像すると、このような割り当てを考えてしまうかもしれない。 すると当然ながら「ある地点には矩形領域が二つ（あるいはたった一つ）しか無い」かつそのために「中央 1/3 領域とは限らない」ケースが考えられる。（アイスランドとか）
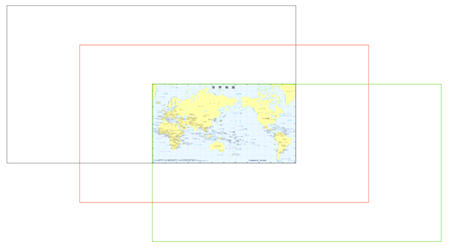	そのため、この「シフトした 3 プレーン Geohash」では最大粒度の矩形領域をまずこのような形から始める必要がある。

世界地図は総務省統計局・政策統括官・統計研修所ホームページから転載